Classification Algorithms

It is not a good idea to apply linear regression to classification problems.

Examples of classification problems.

• Predict if an email is spam or not.
• Predict if a transaction is fraud or not.
• Predict if a tumor is benign or not.

If possible answer is one of two, then it is a binary classification problem.

Logistic Regression

Hypothesis: h_θ(x) = g(z)

• z = θ^Tx
  
• g(z) = 1/(1+e^-z)
• g is called sigmoid or logistic function which asymptotes at 0 and 1
• Hypothesis function h gives the probability that output is 1.
• So if h_θ(x) = 0.7, it means that it is 70% chance that output is 1, and 30% chance that it is 0.

Decision boundary

• A way to convert the analog output function, to discrete.
• h_θ(x) >= 0.5 -> y = 1
• h_θ(x) < 0.5 -> y = 0
• g(z) >= 0.5 when z >= 0 when θ^Tx >= 0

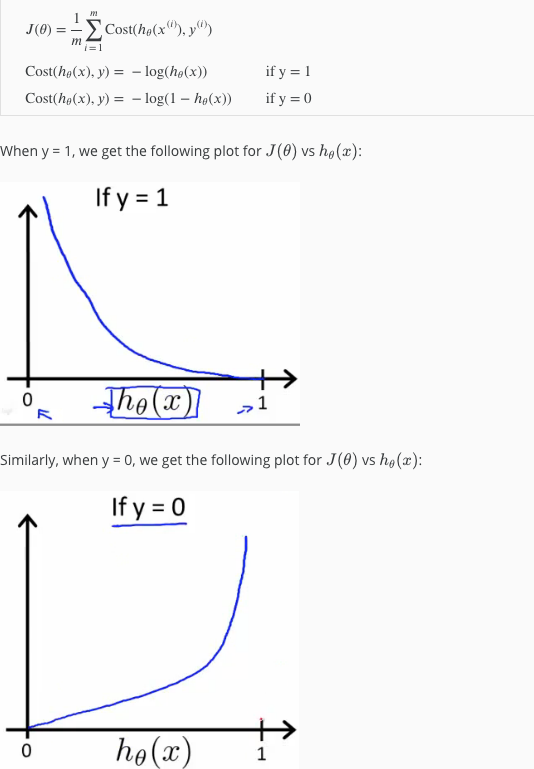
Cost function

Optimization Algorithms

• Gradient descent
• Conjugate gradient
• BFGS
• L-BFGS

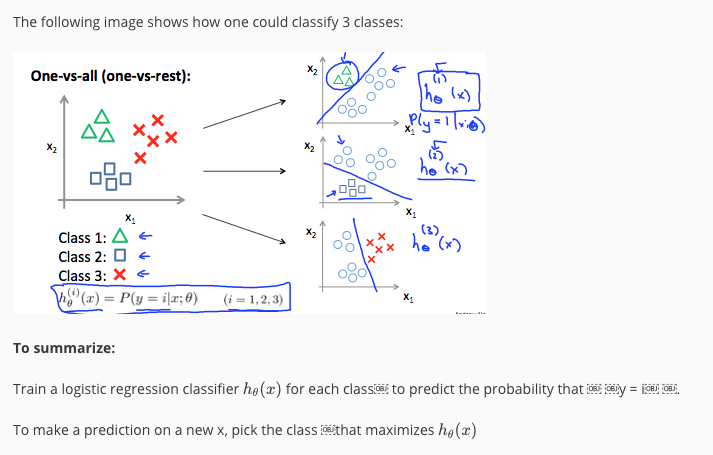
Multi-class classification

Over and under fitting.

Under-fitting

• When a hypothesis function does not fit the training set well.
• Errors are quite high.
• Usually fixed by changing hypothesis function by including higher order polynomials or new features.

Over-fitting

• When a hypothesis function fits training set too well, but fails to predict future outcomes for yet unseen data.
• Happens when there are too many features or hypothesis contains too many higher order polynomials.
• While trying to reduce error rate as much as possible, it ends up creating a function which does not product any errors for training set, but is a overly restrictive predictive function.
• Fixed by regularizing.
• By introducing a very small error in every iteration for each parameter, θ, gives a set of parameter functions which fit the training set well, but also predict future outcomes well.
• Over fitting is possible for linera and logistic regression, regularization applies to both of them.